哈克流变仪HAAKE RS600在胶粘剂环氧树脂中的流变性表征

一般情况下固化反应速率方程为 [ 4] :

式中: A—— 固化度; t —— 反应时间; A ——指前因子;E ——固化活化能; R ——普适气体常数; T —— 绝对温度: f ( α) ——机理函数。

Ozawa 方程为求得固化活化能提供了一个可靠的方式。其表达式为:

通过上式就可以得到固化反应活化能 E, 其值为59141 kJ/ mol。定义两个特殊的函数方程 [5] :

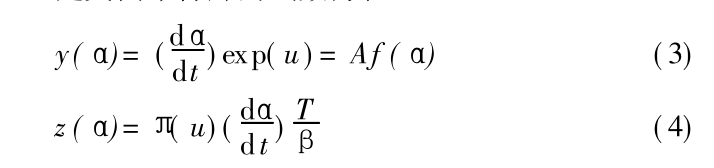
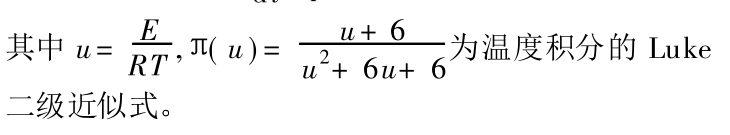
将不同升温速率下的 y (α) 和z( α) , 在( 0, 1) 范围内进行标准化。设 αp 是 DSC 曲线放热峰出现极值处所对应的固度, αM 是 y( α​)出现极值处所对应的固化度,α∞ P 是 z ( α)出现极值处所对应的固化度。当 αM< αp , α∞ P≠ 0.633, 且三个参数都不依赖于升温速率 β时, 函数 f ( α)能够用 Sestal- Berggren 两参数自催化模型表示:

通过上式将作图, 并进行线性拟合, 所得斜率是动力学参数 n, 截距是lnA , 将计算的 n 值代入( 6) 式就可以得到 m 值, 这样就可以求出固化反应速率方程的各个参数, 从而确定了固化反应的速率方程。

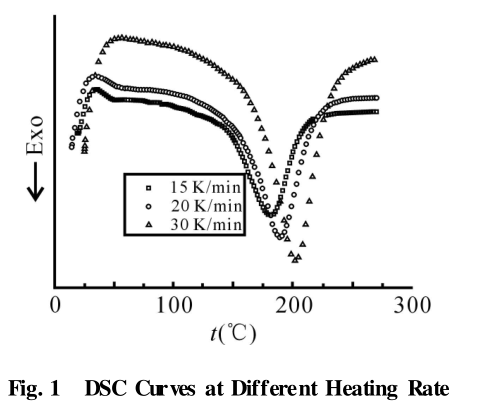
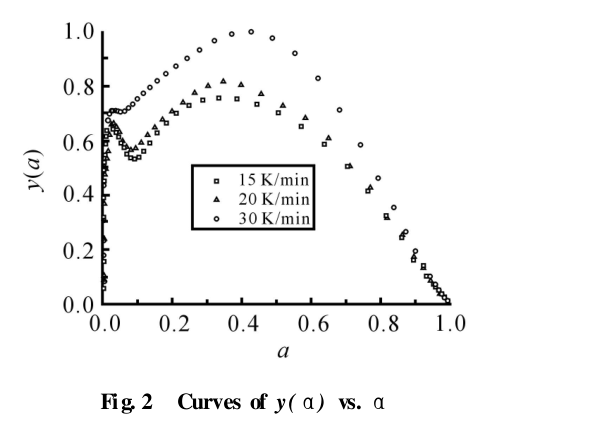
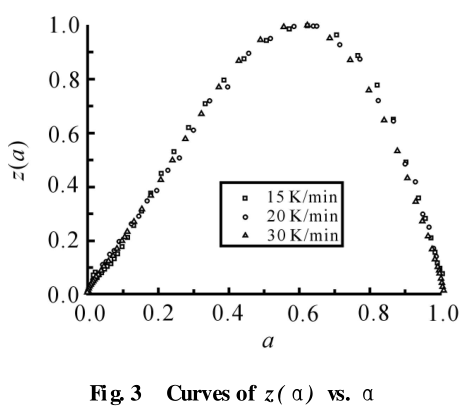
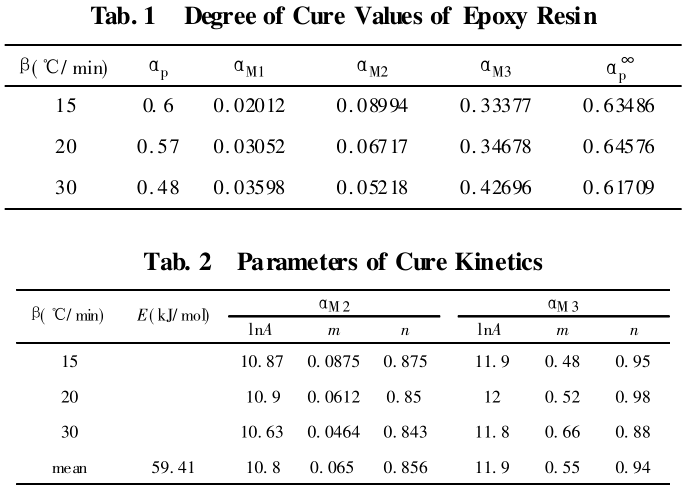
2. 1. 2 实验结果与分析: Fig. 1 是 AG-70 环氧树脂体系在不同升温速率下的 DSC 曲线, 可发现随着升温速率的增加, 树脂体系开始发生固化的温度升高, 放热峰向高温方向移动, 放热时间缩短, 放热发生滞后。从上面的理论分析可得到函数 y ( α) 和 z( α) 与固化度 A之间的关系如 Fig. 2、Fig. 3 所示。从 Fig. 2中可看出,随着固化度的增加, 函数 y ( α) 出现三个极值, 这说明函数 y( A)存在多个特征值。而函数 z(α) 则随着固化度的增加只出现一个极值。将出现的特殊固化度值分别列于 Tab. 1 中。y( α)出现了三个不同极值, 极值的选定对模型预测结果会产生不同影响, 由于 αM 1 太小而忽略, 对极值 αM2 、αM 3 分别进行计算, 其计算结果列于 Tab. 2 中。

将 Tab. 2 中的数据分别代入式( 1) 和式( 5) , 就可以分别得到固化反应速率方程。

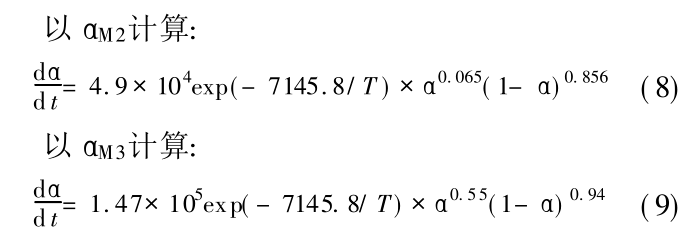
2. 1. 2 实验结果与分析: Fig. 1 是 AG-70 环氧树脂体系在不同升温速率下的 DSC 曲线, 可发现随着升温速率的增加, 树脂体系开始发生固化的温度升高, 放热峰向高温方向移动, 放热时间缩短, 放热发生滞后。从上面的理论分析可得到函数 y ( α) 和 z( α) 与固化度 A之间的关系如 Fig. 2、Fig. 3 所示。从 Fig. 2中可看出,随着固化度的增加, 函数 y ( α) 出现三个极值, 这说明函数 y( A)存在多个特征值。而函数 z(α) 则随着固化度的增加只出现一个极值。将出现的特殊固化度值分别列于 Tab. 1 中。y( α)出现了三个不同极值, 极值的选定对模型预测结果会产生不同影响, 由于 αM 1 太小而忽略, 对极值 αM2 、αM 3 分别进行计算, 其计算结果列于 Tab. 2 中。

将 Tab. 2 中的数据分别代入式( 1) 和式( 5) , 就可以分别得到固化反应速率方程。

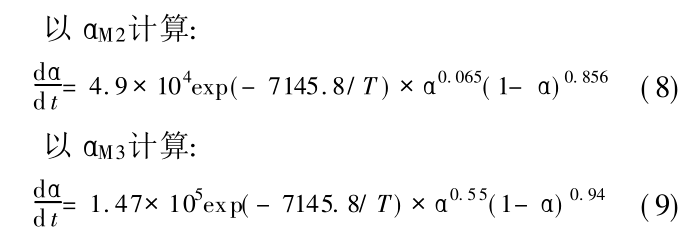
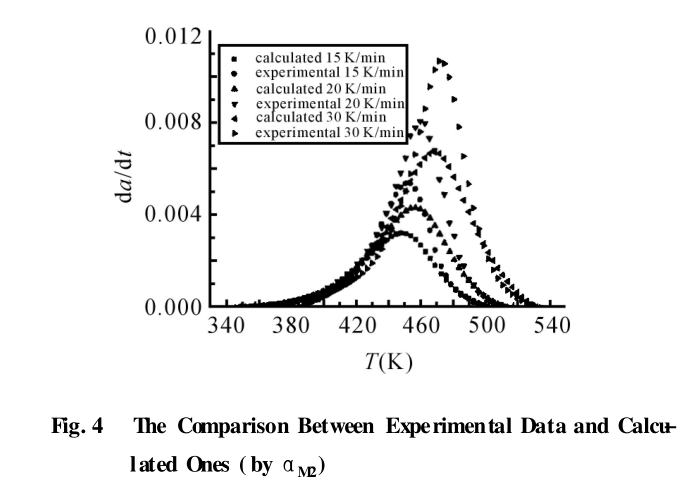
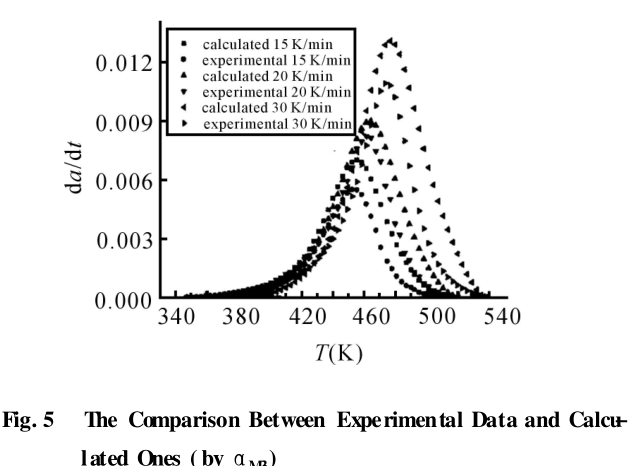
由以上两式确定的理论计算结果和实验计算得到的结果进行比较, 如 Fig. 4、Fig. 5 所示。从Fig. 4 中可看出, 当固化反应速率较大时, 模型预测结果不准确,但在低温和高温时模型的预测结果很好。在 Fig. 5中, 在固化反应速率曲线峰值左边预测结果较好, 但右边的预测误差较大。

2. 2 凝胶模型特性研究

2. 2. 1 理论分析: 环氧树脂体系会随着温度的升高而发生固化反应, 在某一温度下树脂体系分子链迅速缠结形成三维网状结构而使得体系的黏度会突然增大, 产生凝胶现象, 此时温度就是凝胶温度。文献中出现的凝胶点的判断方法一般有以下几种 [6] : 储能模量G‘和损耗模量 G‘’的交点; 损耗因子 tan D曲线曲率最大值处所对应的点; 损耗因子 tan D值与频率无关的起始点; 储能模量 G’与基线的交点。本文中选择前面两种方法来确定凝胶点, 并进行对比。当树脂体系固化到固化为 α gel 时, 对( 1) 式进行变形并积分可得:

从上式可知, 只要在恒温条件下确定凝胶时间, 就可以得到凝胶模型方程 [ 7] 。

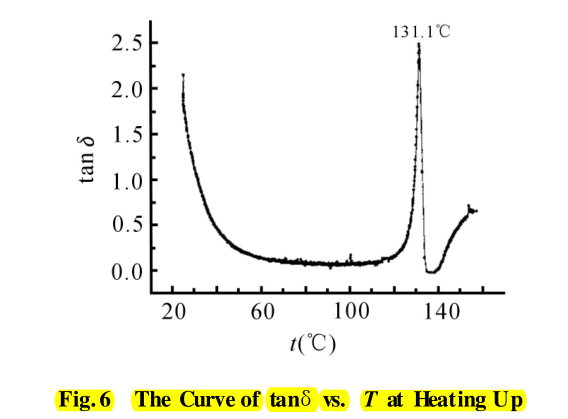
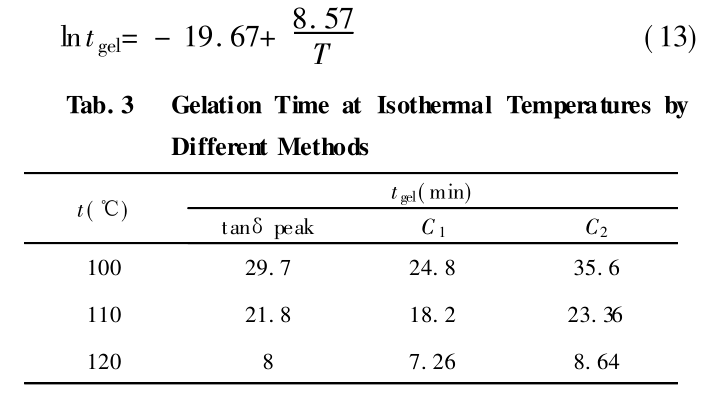
2. 2. 2 实验结果与分析: Fig. 6 是环氧树脂体系在升温过程中的损耗因子 tanD随温度的变化曲线, 从图中可以看出, 曲线在131.1℃处出现一极值, 说明环氧树脂体系在131.1℃处发生凝胶现象, 这比用 DSC 方法获得的凝胶点温度 127.3℃ 高出 3.8℃ 。从实验结果发现, 储能模量 G'和损耗模量 G''的交点有两个。从恒温测试的数据得到不同方法计算的凝胶时间 t gel 列于Tab. 3 中, C 1 、C 2 分别表示储能模量 G'和损耗模量 G''的第一、第二个交点。T ab. 3 中, 无论采用何种方法计算的凝胶时间都随着恒温温度的升高而下降,C 1 值比损耗因子 tanD的峰值低, C 2 值比损耗因子tanD的峰值高, 粗略估计, 损耗因子 tanD的峰值是C 1 、C 2 的算术平均值。

交点 C 1 值与用 DSC 方法得到的凝胶温度值最接近, 故取 T ab. 3 中的 C 1 值为凝胶点, 以( 12) 式为依据, 将凝胶时间对数与温度倒数作图, 并进行线性回归, 可得温度与凝胶时间的关系表达式为:

3 结论

( 1) 用升温 DSC 研究了AG-70 环氧树脂体系在室温至 275 ℃ 范围内的固化反应动力学。结果表明, 该树脂体系的固化反应符合自催化反应模型, 运用Malek 最大概然法求取了模型中的固化反应动力学参数, 并得到了两组固化反应动力学方程。将模型的预测结果与实验数据进行了比较。

( 2) 用 RS600 旋转流变仪测试了树脂体系在升温和恒温条件下的流变性能, 采用两种不同的方式确定了凝胶温度点, 用恒温条件下获得的凝胶时间点为依据, 计算出了凝胶模型, 可用于指导工艺过程。

参考文献:

[ 1] Rosu D, Mustata F, Cascaval C N. Investigation of the curing reac-tions of some multifunctional epoxy resin using differential calorimetry[ J] . Thermochimica Acta, 2001, 370: 105-110.

[ 2] Rosu D, Cascaval C N, M ustata F, et al . Cure kinetics of epoxyresin studied by non-isothermal DSC data[ J] . T hermochimica Acta,2002, 383: 119-127.

[ 3] Chaemy M, Riahy M H. Kinetics of anhydride and polyamide curingof bisphenol a-based diglycidyl ether using DSC [ J] . Eur. Polym.J. , 1996, 32( 10) : 1207-1212.

[ 4] Moon-Kwang U M, Daniel I M , Hwang B S. A study of cure kinet -ics by the use of dynamic differential scanning calorimetry [ J] . Com-pos. Sci. T echnol. , 2002, 62: 29-40.

[ 5] Yousefi A, Lafleur P G . Kinetic studies of thermoset cure reactions:A review [ J] . Polym. Compos. , 1997, 18( 2) : 157-167.

[ 6] Laza J M, Julian C A, Larrauri E, et al. Thermal scanningrheometer analysis of curing kinetic of an epoxy resin: 2. an amine ascuring agent [ J] . Polymer, 1998, 40: 35-45.

[ 7] Mortimer S, Ryan A J, Stanford J L. Rheological behavior and ge-lpoint determination for a model Lewis acid-initiated chain growth e-poxy resin [ J] . Macromolecules, 2001, 34: 2973- 2980.